04 May 2020
The Animation Compression Library v1.3 introduced support for compressing animated floating point tracks but it wasn’t until now that I managed to get around to trying it inside the Unreal Engine 4 Plugin. Scalar tracks are used in various ways from animating the Field Of View to animating Inverse Kinematic blend targets. While they have many practical uses in modern video games, they are most commonly used to animate morph targets (aka blend shapes) in facial and cloth animations.
TL;DR: By using the morph target deformation information, we can better control how much precision each blend weight needs while yielding a lower memory footprint.
How do morph targets work?
Morph targets are essentially a set of meshes that get blended together per vertex. It is a way to achieve vertex based animation. Let’s use a simple triangle as an example:
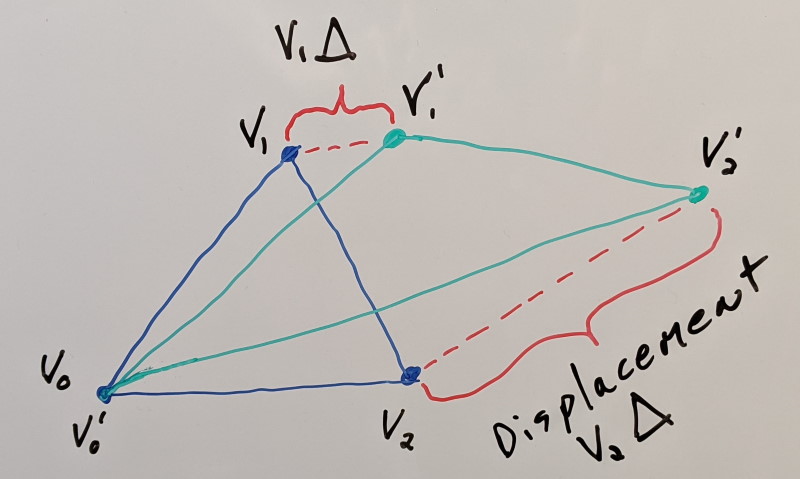
In blue we have our reference mesh and in green our morph target. To animate our vertices, we apply a scaled displacement to every vertex. This scale factor is called the blend weight. Typically it lies between 0.0 (our reference mesh) and 1.0 (our target mesh). Values in between end up being a linear combination of both:
final vertex = reference vertex + (target vertex - reference vertex) * blend weight
Each morph target is thus controlled by a single blend weight and each vertex can end up having a contribution from multiple targets. With our blend weights being independent, we can compress them as a set of floating point curves. This is typically done by specifying a desired level of precision to retain on each curve. However, in practice this can be hard to control: blend weights have no units.
At the time of writing:
- Unreal Engine 4 leaves its curves in a compact raw form (a spline) by default but they can be optionally compressed with various codecs.
- Unity, Lumberyard, and CRYENGINE do not document how they are stored and they do not appear to expose a way to further compress them (as far as I know).
All of this animated data does add up and it can benefit from being compressed. In order to achieve this, the UE4 ACL plugin uses an intuitive technique to control the resulting quality.
Compressing blend weights
Our animated blend weights ultimately yield a mesh deformation. Can we use that information to our advantage? Let’s take a closer look at the math behind morph targets. Here is how each vertex is transformed:
final vertex = reference vertex + (target vertex - reference vertex) * blend weight
As we saw earlier, (target vertex - reference vertex) is the displacement delta to apply to achieve our deformation. Let’s simplify our equation a bit:
final vertex = reference vertex + vertex delta * blend weight
Let’s plug in some displacement numbers with some units and see what happens.
| Reference Position |
Target Position |
Delta |
| 5 cm |
5 cm |
0 cm |
| 5 cm |
5.1 cm |
0.1 cm |
| 5 cm |
50 cm |
45 cm |
Let us assume that at a particular moment in time, our raw blend weight is 0.2. Due to compression, that value will change by the introduction of a small amount of imprecision. Let’s see what happens if our lossy blend weight is 0.22 instead.
| Delta |
Delta * Raw Blend Weight |
Delta * Lossy Blend Weight |
Error |
| 0 cm |
0 cm |
0 cm |
0 cm |
| 0.1 cm |
0.02 cm |
0.022 cm |
0.002 cm |
| 45 cm |
9 cm |
9.9 cm |
0.9 cm |
From this, we can observe some important facts:
- When our vertex doesn’t move and has no displacement delta, the error introduced doesn’t matter.
- The error introduced is linearly proportional to the displacement delta: when the error is fixed, a small delta will have a small amount of error while a large delta will have a large amount of error.
This means that it is not suitable to set a single precision value (in blend weight space) for all our blend weights. Some morph targets require more precision than others and ideally we would like to take advantage of that fact.
Specifying the amount of precision that a blend weight should have isn’t easy if we don’t know how much deformation it ultimately drives. A better way to specify how much precision we need is by specifying it in meaningful units. If we assume that we want our vertices to have a precision of 0.01 cm instead, how much precision do their blend weights need?
blend weight precision = vertex precision / vertex displacement delta
Notice how the vertex precision and vertex displacement delta units cancel out.
| Delta |
Blend Weight Precision |
| 0 cm |
Division by zero! |
| 0.1 cm |
0.1 |
| 45 cm |
0.00022 |
When a vertex doesn’t move, it doesn’t matter what precision our blend weight retains since the final vertex position will be identical regardless. However, smaller displacements require less precision while larger displacements require more precision retained.
This is what the ACL plugin does: when a Skeletal Mesh is provided to the compression codec, ACL will use a vertex displacement precision value instead of a generic scalar track precision value. This is intuitive to tune for an artist because the units now have meaning: we can easily find out how much 0.01 cm represents within the context of our 3D model. Underneath the hood, this translates into unique precision requirements tailored to each morph target blend weight curve. This allows ACL to attain an even lower memory footprint while providing a strict guarantee on the visual fidelity of the animated deformations.
A Boy and His Kite
In order to test this out, I used the GDC 2015 demo from Epic: A Boy and His Kite. The demo is available for free on the Unreal Marketplace under the Learning section.
It shows a boy running through a landscape along with his kite. He contains 811 animated curves within each of the 31 animation sequences that comprise the full cinematic. 692 of those curves end up driving morph targets for his facial and clothing deformations. Some of the shots have the camera very close to his face and as such retaining as much quality as possible is critical.
I decided to compare 5 codecs:
- Compressed Rich Curves with an error threshold of 0.0 (default within UE 4.25)
- Compressed Rich Curves with an error threshold of 0.001
- Uniform Sampling
- ACL with a generic precision of 0.001
- ACL with a generic precision of 0.001 and a morph target deformation precision of 0.01 cm
The Compressed Rich Curves and Uniform Sampling codecs are built into UE4 and provide a trade-off between memory and speed. The rich curves will tend to have a lower memory footprint but evaluating them at runtime is slower than when uniform sampling is used.
ACL uses uniform sampling internally for very fast evaluation but it is also much more aggressive with its compression.
| |
Compressed Size |
Compression Rate |
| Compressed Rich Curves 0.0 |
3620.66 KB |
1.0x (baseline) |
| Compressed Rich Curves 0.001 |
1458.77 KB |
2.5x smaller |
| Uniform Sampling |
2052.82 KB |
1.8x smaller |
| ACL 0.001 |
540.24 KB |
6.7x smaller |
| ACL with morph 0.01 cm |
381.10 KB |
9.5x smaller |
I manually inspected the visual fidelity of each codec and everything looked flawless. By leveraging our knowledge of the individual morph target deformations, ACL manages to reduce the memory footprint by an extra 159.14 KB (29%).
The new curve compression will be available shortly in the ACL plugin v0.6 (suitable for UE 4.24) as well as v1.0 (suitable for UE 4.25 and later). The ACL plugin v1.0 isn’t out yet but it will come to the Unreal Marketplace as soon as UE 4.25 is released.
18 Nov 2019
After 7 months of work, the Animation Compression Library has finally reached v1.3 along with an updated v0.5 Unreal Engine 4 plugin. Notable changes in this release include:
- Added support for VS2019, GCC 9, clang7, and Xcode 11
- Optimized compression and decompression significantly
- Added support for multiple root bones
- Added support for scalar track compression
Compared to UE 4.23.1, the ACL plugin compresses up to 2.9x smaller, is up to 4.7x more accurate, up to 52.9x faster to compress, and up to 6.8x faster to decompress (results may vary depending on the platform and data).
This latest release is a bit more accurate than the previous one and it also reduces the memory footprint by about 4%. Numbers vary a bit but decompression is roughly 1.5x faster on every platform.
Realtime compression
The compression speed improvements are massive. Compared to the previous release, it is over 2.6x faster!
| |
ACL v1.3 |
ACL v1.2 |
| CMU |
2m 22.3s (10285.52 KB/sec) |
6m 9.71s (3958.99 KB/sec) |
| Paragon |
10m 23.05s (7027.87 KB/sec) |
28m 56.48s (2521.62 KB/sec) |
| Matinee fight scene |
4.89s (13074.59 KB/sec) |
20.27s (3150.43 KB/sec) |
It is so fast that when I tried it in Unreal Engine 4 and the popup dialog showed instantaneously after compression, I thought something was wrong. I got curious and decided to take a look at how fast it is for individual clips. The results were quite telling. In the Carnegie-Mellon University motion capture database, 50% of the clips compress in less than 29ms, 85% take less than 114ms, and 99% compress in 313ms or less. In Paragon, 50% of the clips compress in less than 31ms, 85% take less than 128ms, and 99% compress in 1.461 seconds or less. Half of ordinary animations compress fast enough to do so in realtime!
I had originally planned more improvements to the compression speed as part of this release but ultimately opted to stop there for now. I tried to switch from Arrays of Structures to Structures of Arrays and while it was faster, the added complexity was not worth the very minimal gain. There remains lots of room for improvement though and the next release should be even faster.
What’s next
The next release will be a major one: v2.0 is scheduled around Summer 2020. A number of significant changes and additions are planned.
While Realtime Math was integrated this release for the new scalar track compression API, the next release will see it replace all of the math done in ACL. Preliminary results show that it will speed up compression by about 10%. This will reduce significantly the maintenance burden and speed up CI builds. This will constitute a fairly minor API break. RTM is already included within every release of ACL (through a sub-module). Integrations will simply need to add the required include path as well as change the few places that interface with the library.
The error metric functions will also change a bit to allow further optimization opportunities. This will constitute a minor API break as well if integrations have implemented their own error metric (which is unlikely).
So far, ACL is what might be considered a runtime compression format. It was designed to change with every release and as such requires recompression whenever a new version comes out. This isn’t a very big burden as more often than not, game engines already recompress animations on demand, often storing raw animations in source control. Starting with the next release, backwards compatibility will be introduced. In order to do this, the format will be standardized, modernized, and documented. The decompression code path will remain optimal through templating. This step is necessary to allow ACL to be suitable for long term storage. As part of this effort, a glTF extention will be created as well as tools to pack and unpack glTF files.
Last but not least, a new javascript/web assembly module will be created in order to support ACL on the modern web. Through the glTF extension and a ThreeJS integration, it will become a first class citizen in your browser.
ACL is already in use on millions of consoles and mobile devices today and this next major release will make its adoption easier than ever.
If you use ACL and would like to help prioritize the work I do, feel free to reach out and provide feedback or requests!
Thanks to GitHub Sponsors, you can sponsor me! All funds donated will go towards purchasing new devices to optimize for as well as other related costs (like coffee). The best way to ensure that ACL continues to move forward is to sponsor me for specific feature work, custom integrations, through GitHub, or some other arrangement.
14 Nov 2019
Today Realtime Math has finally reached v1.1.0! This release brings a lot of good things:
- Added support for Windows ARM64
- Added support for VS2019, GCC9, clang7, and Xcode 11
- Added support for Intel FMA and ARM64 FMA
- Many optimizations, minor fixes, and cleanup
I spent a great deal of time optimizing the quaternion arithmetic for NEON and SSE and as a result, many functions are now among the fastest out there. In order to make sure not to introduce regressions, the Google Benchmark library has been integrated and allows me to quickly whip up tests to try various ideas and variants.
RTM will be used in the upcoming Animation Compression Library release for the new scalar track compression API. The subsequent ACL release will remove all of its internal math code and switch everything to RTM. Preliminary tests show that it speeds up its compression by about 10%.
Is Intel FMA worth it?
As part of this release, support for AVX2 and FMA was added. Seeing how libraries like DirectX Math already use FMA, I expected it to give a measurable performance win. However, on my Haswell MacBook Pro and my Ryzen 2950X desktop, it turned out to be significantly slower. As a result of these findings, I opted to not use FMA (although the relevant defines are present and handled). If you are aware of a CPU where FMA is faster, please reach out!
It is also worth noting that typically when Fast Math type compiler optimizations are enabled, FMA instructions are often automatically generated when it detects a pattern where they can be used. RTM explicitly disables this behavior with Visual Studio (by forcing Precise Math with a pragma) and as such even when it is enabled, the functions retain the SSE/AVX instructions that showed the best performance.
RTM, DirectX Math, and many other libraries make extensive use NEON SIMD intrinsics. However, while measuring various implementation variants for quaternion multiplication I noticed that using simple scalar math is considerably faster on both ARMv7 and ARM64 on my Pixel 3 phone and my iPad. Going forward I will make sure to always measure the scalar code path as a baseline.
Compiler bugs
Surprisingly, RTM triggered 3 compiler code generation bugs this year. #34 and #35 in VS2019 as well as #37 in clang7. As soon as those are fixed and validated by continuous integration, I will release a new version (minor or patch).
What’s next
The development of RTM is largely driven by my work with ACL. If you’d like to see specific things in the next release, feel free to reach out or to create GitHub issues and I will prioritize them accordingly. As always, contributions welcome!
Thanks to GitHub Sponsors, you can sponsor me! All funds donated will go towards purchasing new devices to optimize for as well as other related costs (like coffee).
22 Oct 2019
Today it’s time to talk about another floating point arithmetic trick that sometimes can come in very handy with SSE2. This trick isn’t novel, and I don’t often get to use it but a few days ago inspiration struck me late at night in the middle of a long 3 hour drive. The results inspired this post.
I’ll cover three functions that use it for quaternion arithmetic which have already been merged into the Realtime Math (RTM) library as well as the Animation Compression Library (ACL). ACL uses quaternions heavily and I’m always looking for ways to make them faster.
TL;DR: With SSE2, XOR (and other logical operators) can be leveraged to speed up common floating point operations.
XOR: the lesser known logical operator
Most programmers are familiar with AND, OR, and NOT logical operators. They form the bread and butter of everyday programming. And while we all learn about their cousin XOR, it doesn’t come in handy anywhere near as often. Here is a quick recap of what it does.
| A |
B |
A XOR B |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
We can infer a few interesting properties from it:
- Any input that we apply XOR to with zero yields the input
- XOR can be used to flip a bit from
true to false or vice versa by XOR-ing it with one
- Using XOR when both inputs are identical yields zero (every zero bit remains zero and every one bit flips to zero)
Exclusive OR comes in handy mostly with bit twiddling hacks when squeezing every cycle counts. While it is commonly used with integer inputs, it can also be used with floating point values!
XOR with floats
SSE2 contains support for XOR (and other logical operators) on both integral (_mm_xor_si128) and floating point values (_mm_xor_ps). Usually when you transition from the integral domain to the floating point domain of operations on a register (or vice versa), the CPU will incur a 1 cycle penalty. By implementing a different instruction for both domains, this hiccup can be avoided. Logical operations can often execute on more than one execution port (even on older hardware) which can enable multiple instructions to dispatch in the same cycle.
The question then becomes, when does it make sense to use them?
Quaternion conjugate
For a quaternion A where A = [x, y, z] | w with real ([x, y, z]) and imaginary (w) parts, its conjugate can be expressed as follow: conjugate(A) = [-x, -y, -z] | w. The conjugate simply flips the sign of each component of the real part.
The most common way to achieve this is by multiplying a constant just like DirectX Math and Unreal Engine 4 do.
quatf quat_conjugate(quatf input)
{
constexpr __m128 signs = { -1.0f, -1.0f, -1.0f, 1.0f };
return _mm_mul_ps(input, signs);
}
This yields a single instruction (the constant will be loaded from memory as part of the multiply instruction) but we can do better. Flipping the sign bit can also be achieved by XOR-ing our input with the sign bit. To avoid flipping the sign of the w component, we can simply XOR it with zero which will leave the original value unchanged.
quatf quat_conjugate(quatf input)
{
constexpr __m128 signs = { -0.0f, -0.0f, -0.0f, 0.0f };
return _mm_xor_ps(input, signs);
}
Again, this yields a single instruction but this time it is much faster. See full results here but on my MacBook Pro it is 33.5% faster!
Quaternion interpolation
Linear interpolation for scalars and vectors is simple: result = ((end - start) * alpha) + start.
While this can be used for quaternions as well, it breaks down if both quaternions are not on the same side of the hypersphere. Both quaternions A and -A represent the same 3D rotation but lie on opposite ends of the 4D hypersphere represented by unit quaternions. In order to properly handle this case, we first need to calculate the dot product of both inputs being interpolated and depending its sign, we must flip one of the inputs so that it can lie on the same side of the hypersphere.
In code it looks like this:
quatf quat_lerp(quatf start, quatf end, float alpha)
{
// To ensure we take the shortest path, we apply a bias if the dot product is negative
float dot = vector_dot(start, end);
float bias = dot >= 0.0f ? 1.0f : -1.0f;
vector4f rotation = vector_neg_mul_sub(vector_neg_mul_sub(end, bias, start), alpha, start);
return quat_normalize(rotation);
}
The double vector_neg_mul_sub trick was explained in a previous blog post.
As mentioned, we take the sign of the dot product to calculate a bias and simply multiply it with the end input. This can be achieved with a compare instruction between the dot product and zero to generate a mask and using that mask to select between the positive and negative value of end. This is entirely branchless and boils down to a few instructions: 1x compare, 1x subtract (to generate -end), 1x blend (with AVX to select the bias), and 1x multiplication (to apply the bias). If AVX isn’t present, the selection is done with 3x logical operation instructions instead. This is what Unreal Engine 4 and many others do.
Here again, we can do better with logical operators.
quatf quat_lerp(quatf start, quatf end, float alpha)
{
__m128 dot = vector_dot(start, end);
// Calculate the bias, if the dot product is positive or zero, there is no bias
// but if it is negative, we want to flip the 'end' rotation XYZW components
__m128 bias = _mm_and_ps(dot, _mm_set_ps1(-0.0f));
__m128 rotation = _mm_add_ps(_mm_mul_ps(_mm_sub_ps(_mm_xor_ps(end, bias), start), _mm_set_ps1(alpha)), start);
return quat_normalize(rotation);
}
What we really want to achieve is to do nothing (use end as-is) if the sign of the bias is zero and to flip the sign of end if the bias is negative. This is a perfect fit for XOR! All we need to do is XOR end with the sign bit of the bias. We can easily extract it with a logical AND instruction and a mask of the sign bit. This boils down to just two instructions: 1x logical AND and 1x logical XOR. We managed to remove expensive floating point operations while simultaneously using fewer and cheaper instructions.
Measuring is left as an exercise for the reader.
Quaternion multiplication
While the previous two use cases have been in RTM for some time now, this one is brand new and is what crossed my mind the other night: quaternion multiplication can use the same trick!
Multiplying two quaternions with scalar arithmetic is done like this:
quatf quat_mul(quatf lhs, quatf rhs)
{
float x = (rhs.w * lhs.x) + (rhs.x * lhs.w) + (rhs.y * lhs.z) - (rhs.z * lhs.y);
float y = (rhs.w * lhs.y) - (rhs.x * lhs.z) + (rhs.y * lhs.w) + (rhs.z * lhs.x);
float z = (rhs.w * lhs.z) + (rhs.x * lhs.y) - (rhs.y * lhs.x) + (rhs.z * lhs.w);
float w = (rhs.w * lhs.w) - (rhs.x * lhs.x) - (rhs.y * lhs.y) - (rhs.z * lhs.z);
return quat_set(x, y, z, w);
}
Floating point multiplications and additions being expensive, we can reduce their number by converting this to SSE2 and shuffling our inputs to line everything up. A few shuffles can line the values up for our multiplications but it is clear that in order to use addition (or subtraction), we have to flip the signs of a few components. Again, DirectX Math does just this (and so does Unreal Engine 4).
quatf quat_mul(quatf lhs, quatf rhs)
{
constexpr __m128 control_wzyx = { 1.0f,-1.0f, 1.0f,-1.0f };
constexpr __m128 control_zwxy = { 1.0f, 1.0f,-1.0f,-1.0f };
constexpr __m128 control_yxwz = { -1.0f, 1.0f, 1.0f,-1.0f };
__m128 r_xxxx = _mm_shuffle_ps(rhs, rhs, _MM_SHUFFLE(0, 0, 0, 0));
__m128 r_yyyy = _mm_shuffle_ps(rhs, rhs, _MM_SHUFFLE(1, 1, 1, 1));
__m128 r_zzzz = _mm_shuffle_ps(rhs, rhs, _MM_SHUFFLE(2, 2, 2, 2));
__m128 r_wwww = _mm_shuffle_ps(rhs, rhs, _MM_SHUFFLE(3, 3, 3, 3));
__m128 lxrw_lyrw_lzrw_lwrw = _mm_mul_ps(r_wwww, lhs);
__m128 l_wzyx = _mm_shuffle_ps(lhs, lhs,_MM_SHUFFLE(0, 1, 2, 3));
__m128 lwrx_lzrx_lyrx_lxrx = _mm_mul_ps(r_xxxx, l_wzyx);
__m128 l_zwxy = _mm_shuffle_ps(l_wzyx, l_wzyx,_MM_SHUFFLE(2, 3, 0, 1));
__m128 lwrx_nlzrx_lyrx_nlxrx = _mm_mul_ps(lwrx_lzrx_lyrx_lxrx, control_wzyx); // flip!
__m128 lzry_lwry_lxry_lyry = _mm_mul_ps(r_yyyy, l_zwxy);
__m128 l_yxwz = _mm_shuffle_ps(l_zwxy, l_zwxy,_MM_SHUFFLE(0, 1, 2, 3));
__m128 lzry_lwry_nlxry_nlyry = _mm_mul_ps(lzry_lwry_lxry_lyry, control_zwxy); // flip!
__m128 lyrz_lxrz_lwrz_lzrz = _mm_mul_ps(r_zzzz, l_yxwz);
__m128 result0 = _mm_add_ps(lxrw_lyrw_lzrw_lwrw, lwrx_nlzrx_lyrx_nlxrx);
__m128 nlyrz_lxrz_lwrz_wlzrz = _mm_mul_ps(lyrz_lxrz_lwrz_lzrz, control_yxwz); // flip!
__m128 result1 = _mm_add_ps(lzry_lwry_nlxry_nlyry, nlyrz_lxrz_lwrz_wlzrz);
return _mm_add_ps(result0, result1);
}
The code this time is a bit harder to read but here is the gist:
- We need 7x shuffles to line everything up
- With everything lined up, we need 4x multiplications and 3x additions
- 3x multiplications are also required to flip our signs ahead of each addition (which conveniently can also be done with fused-multiply-add)
I’ll omit the code for brevity but by using -0.0f and 0.0f as our control values to flip the sign bits with XOR instead, quaternion multiplication becomes much faster. On my MacBook Pro it is 14% faster while on my Ryzen 2950X it is 10% faster! I also measured with ACL to see what the speed up would be in a real world use case: compressing lots of animations. With the data sets I measure with, this new quaternion multiplication accelerates the compression by up to 1.3%.
Most x64 CPUs in use today (including those in the PlayStation 4 and Xbox One) do not yet support fused-multiply-add and when I add support for it in RTM, I will measure again.
Is it safe?
In all three of these examples, the results are binary exact and identical to their reference implementations. Flipping the sign bit on normal floating point values (and infinities) with XOR yields a binary exact result. If the input is NaN, XOR will not yield the same output but it will yield a NaN with the sign bit flipped which is entirely valid and consistent (the sign bit is typically left unused on NaN values).
I also measured this trick with NEON on ARMv7 and ARM64 but sadly it is slower on those platforms (for now). It appears that there is indeed a penalty there for switching between the two domains and perhaps in time it will go away or perhaps something else is slowing things down.
ARM64 already uses fused-multiply-add where possible.
Progress update
It has been almost a year since the first release of RTM. The next release should happen very soon now, just ahead of the next ACL release which will introduce it as a dependency for its scalar track compression API. I am on track to finish both releases before the end of the year.
Thanks to the new GitHub Sponsors program, you can now sponsor me! All funds donated will go towards purchasing new devices to optimize for as well as other related costs (like coffee).
31 Jul 2019
A quick recap: animation clips are formed from a set of time series called tracks. Tracks have a fixed number of samples per second and each track has the same length. The Animation Compression Library retains every sample while Unreal Engine uses the popular method of removing samples that can be linearly interpolated from their neighbors.
The first post showed how removing samples negates some of the benefits that come from segmenting, rendering the technique a lot less effective.
The second post explored how sorting (or not) the retained samples impacts the decompression performance.
The third post took a deep dive into the memory overhead of the three techniques we have been discussing so far:
- Retaining every sample with ACL
- Sorted and unsorted linear sample reduction
This fourth and final post in the series shows exactly how many samples are removed in practice.
How often are samples removed?
In order to answer this question, I instrumented the ACL UE4 plugin to extract how many samples per pose, per clip, and per track were dropped. I then ran this over the Carnegie-Mellon University motion capture database as well as Paragon and Fortnite. I did this while keeping every sample with full precision (quantizing the samples can only make things worse) with and without error compensation (retargeting). The idea behind retargeting is to compensate the error by altering the samples slightly as we optimize a bone chain. While it will obviously be slower to compress than not using it, it should in theory reduce the overall error and possibly allow us to remove more samples as a result.
Note that constant and default tracks are ignored when calculating the number of samples dropped.
| Carnegie-Mellon University |
With retargeting |
Without retargeting |
| Total size |
204.40 MB |
204.40 MB |
| Compression speed |
6487.83 KB/sec |
9756.59 KB/sec |
| Max error |
0.1416 cm |
0.0739 cm |
| Median dropped per clip |
0.13 % |
0.13 % |
| Median dropped per pose |
0.00 % |
0.00 % |
| Median dropped per track |
0.00 % |
0.00 % |
As expected, the CMU motion capture database performs very poorly with sample reduction. By its very nature, motion capture data can be quite noisy as it comes from cameras or sensors.
| Paragon |
With retargeting |
Without retargeting |
| Total size |
575.55 MB |
572.60 MB |
| Compression speed |
2125.21 KB/sec |
3319.38 KB/sec |
| Max error |
80.0623 cm |
14.1421 cm |
| Median dropped per clip |
12.37 % |
12.70 % |
| Median dropped per pose |
13.04 % |
13.41 % |
| Median dropped per track |
2.13 % |
2.25 % |
Now the data is more interesting. Retargeting continues to be slower to compress but surprisingly, it fails to reduce the memory footprint as well as the number of samples dropped. It even fails to improve the compression accuracy.
| Fortnite |
With retargeting |
Without retargeting |
| Total size |
1231.97 MB |
1169.01 MB |
| Compression speed |
1273.36 KB/sec |
2010.08 KB/sec |
| Max error |
283897.4062 cm |
172080.7500 cm |
| Median dropped per clip |
7.11 % |
7.72 % |
| Median dropped per pose |
10.81 % |
11.76 % |
| Median dropped per track |
15.37 % |
16.13 % |
The retargeting trend continues with Fortnite. One possible explanation for these disappointing results is that error compensation within UE4 does not measure the error in the same way that the engine does after compression is done: it does not take into account virtual vertices or leaf bones. This discrepancy leads to the optimizing algorithm thinking the error is lower than it really is.
This is all well and good but how does the full distribution look? Retargeting will be omitted since it doesn’t appear to contribute much.
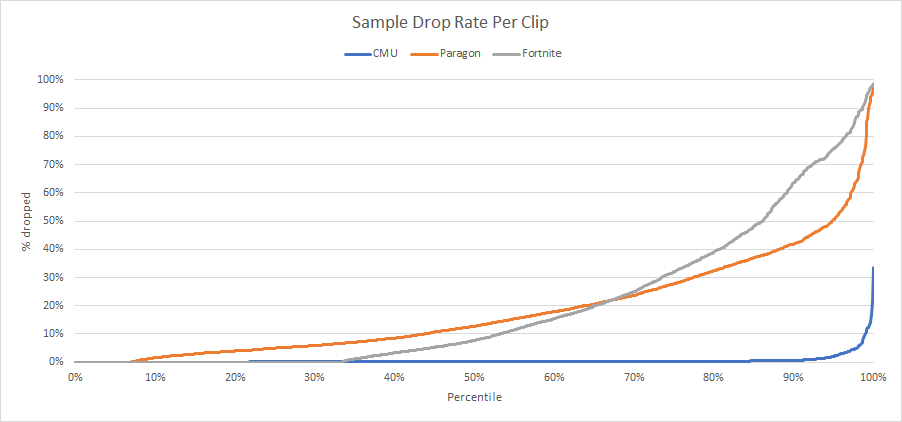
Note that Paragon and Fortnite have ~460 clips (7%) and ~2700 clips (32%) respectively with one or two samples and thus no reduction can happen in those clips.
The graph is quite telling: more often than not we fail to drop enough samples to match ACL with segmenting. Very few clips end up dropping over 35% of their samples: none do in CMU, 18% do in Paragon, and 23% in Fortnite.
This is despite using very optimistic memory overhead estimates. In practice, the overhead is almost always higher than what we used in our calculations and removing samples might negatively impact our quantization bit rates, further increasing the overall memory footprint.
Note that curve fitting might allow us to remove more samples but it would slow down compression and decompression.
Removing samples just isn’t worth it
I have been implementing animation compression algorithms in one form or another for many years now and I have grown to believe that removing samples just isn’t worth it: retaining every sample is the overall best strategy.
Games often play animations erratically or in unpredictable manner. Some randomly seek while others play forward and backward. Various factors control when and where an animation starts playing and when it stops. Clips are often sampled at various sample rates that differ from their runtime playback rates. The ideal default strategy must handle all of these cases equally well. The last thing animators want to do is mess around with compression parameters of individual clips to avoid an algorithm butchering their work.
When samples are removed, sorting what is retained and using a persistent context is a challenging idea in large scale games. Even if decompression has the potential to be the fastest under specific conditions, in practice the gains might not materialize. Regardless, whether the retained samples are sorted or not, metadata must be added to compensate and it eats away at the memory gains achieved. While the Unreal Engine codecs (which use unsorted sample reduction) could be optimized, the amount of cache misses cannot be significantly reduced and ultimately proves to be the bottleneck.
Furthermore, as ACL continues to show, removing samples is not necessary in order to achieve a low and competitive memory footprint. By virtue of having its data simply laid out in memory, very little metadata overhead is required and performance remains consistent and lightning fast. This also dramatically simplifies and streamlines compression as we do not need to consider which samples to retain while attempting to find the optimal bit rate for every track.
It is also worth noting that while we assumed that it is possible to achieve the same bit rates as ACL while removing samples, it might not be the case as the resulting error will combine in subtle ways. Despite being very conservative in our estimates with the sample reduction variants, ACL emerges a clear winner.
That being said, I do have some ideas of my own on how to tackle the problem of efficient sample reduction and maybe someday I will get the chance to try them even if only for the sake of research.
A small note about curves
It is worth nothing that by uniformly sampling an input curve, some amount of precision loss can happen. If the apex of a curve happens between two samples, it will be smoothed out and lost.
The most common curve formats (cubic) generally require 4 values in order to interpolate. This means that the context footprint also increases by a factor of two. In theory, a curve might need fewer samples to represent the same time series but that is not always the case. Animations that come from motion capture or offline simulations such as cloth or hair will often have very noisy data and will not be well approximated by a curve. Such animations might see the number of samples removed drop below 10% as can be seen with the CMU motion capture database.
Curves might also need arbitrary time values that do not fall on uniformly distributed values. When this is the case, the time cannot be quantized too much as it will lower the resulting accuracy, further complicating things and increasing the memory footprint. If the data is non-uniform, a context object is required in order to keep decompression fast and everything I mentioned earlier applies. This is also true of techniques that store their data relative to previous samples (e.g. a delta or velocity change).
Special thanks
I spend a great deal of time implementing ACL and writing about the nuggets of knowledge I find along the way. All of this is made possible, in part, thanks to Epic which is generously allowing me to use the Paragon and Fortnite animations for research purposes. Cody Jones, Martin Turcotte, and Raymond Barbiero continue to contribute code, ideas, and proofread my work and their help is greatly appreciated. Many others have contributed to ACL and its UE4 plugin as well. Thank you for keeping me motivated and your ongoing support!


