Animation Compression: Terminology
26 Oct 2016Animation Sequence or Clip
Central to character animation is our animation sequence. These are also commonly called animation clips and I will use both terms interchangeably.
A clip is composed of several bones and standalone tracks. This post will not focus on standalone tracks since they can typically be represented as fake bones and regardless, all the techniques we will cover could be used to compress them as well as a natural extension.
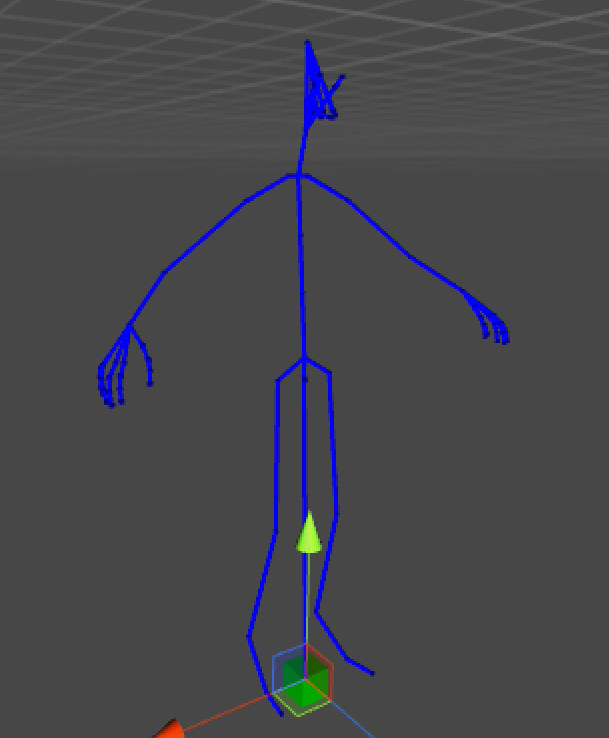
Skeleton
Our character animation sequences will always play back over a rigid skeleton. The skeleton defines a number of bones and their hierarchical relationship (parent/child).
A skeleton has a well defined bind pose. The bind pose represents the default reference pose of the skeleton. For example, the pelvis bone would have a bind pose with a fixed translation offset of 60cm above the ground. The first spine bone would have a small offset above the parent pelvis bone, etc.
A skeleton has a root bone. The root bone is the bone highest in the hierarchy on which all other bones are parented. This is typically the bone that is animated to move characters about the world when the motion is animation driven.
Bone
A bone is commonly composed of at least 2 tracks: rotation and translation. The next post will go into further details about how these are represented in the data.
Also very common is for bones to have a scale value associated. When it is present, bones have a 3rd scale track.
All bones have exactly one parent bone (except the root bone which has none) and optional children.
Bone transform
A bone transform can be represented in a number of ways but for our intents and purposes, we can assume it is a 4x4 affine matrix. These support rotation, translation, and non-uniform scale.
A bone transform can be either in object space or local space.
Track
A track is composed of 1+ keys. All tracks in a raw sequence will have the same number of keys. A sequence with a single key represents a static pose and consequently has an effective length in time of 0 seconds.
Track key
A track key is composed of 1+ components. For example, a translation track would generally have 3 components: X, Y, and Z.
Key component
A key component is a 32 bit float value in its raw form. In practice, standalone tracks could have any value or type (bool, int, etc.) but we will mostly focus on rotation, translation, and scale in this series and these will all use floats.
Key interpolation
Key interpolation is the act of taking two neighbour keys and interpolating a new key at some time T in between. For example, if I have a key at time 0.0s and another at time 0.5s, I can trivially reconstruct a key at time 0.25s by interpolating my two keys.
Because video games are realtime, it is very rare for the game to sync up perfectly with animation sequences, as such nearly every frame will end up interpolating between 2 keys. Consequently, when we sample our clips for playback, we will typically always sample 2 keys to interpolate in between.
Generally speaking, the interpolation will always be linear even for rotations. This is typically safe since keys are assumed to be somewhat close to one another such that linear interpolation will correspond approximately to the shortest path.
Note that some algorithms perform this interpolation implicitly when you sample them: linear key reduction, curve fitting, etc.
Object space
Bone transforms in object space are relative to the whole skeleton. For certain animation clips such as cinematics, they are sometimes animated in world space in which case object space will correspond to world space. When this distinction is relevant, we will explicitly mention it.
Local space
Bone transforms in local space are relative to their parent bone. For the root bone, the local space is equivalent to the object space since it has no parent.
Converting from local space to object space entails multiplying the object space transform of our parent bone by the local space transform of our current bone. Converting from object space to local space is the opposite and requires multiplying the inverse object space transform of our parent bone by the object space transform of our current bone.
Rotation
A rotation represents an orientation at a given point in time. It can be represented in many ways but the two most common are 3x3 matrices and quaternions. Other format exist and will be covered to some extent in future posts.
Translation
A translation represents an offset at a given point in time. It is typically represented at a vector with 3 components.
Scale
A scale is composed of either a single scalar value or a vector with 3 components. The later is used to support non-uniform scaling in which skew and shear are possible. For our purposes, scale will always be a vector with 3 components.
Frame
A frame represents a unit of time. Most games are played at 30 frames per second (FPS) as such every frame has a length of time equal to 1.0s / 30.0 = 0.03333s.
A clip with 2 keys consequently has 1 unit of time that elapses in between. If the first key is at 0.0s and the second key is at 0.5s, we can reconstruct the key position at any time in between by linearly interpolating our keys. A clip with 11 keys, has 10 frames, etc.
The frame rate of the game does need to match the sample rate of animation clips.
Note that in the literature, the term ‘frame’ is sometimes used to mean a transform (e.g. frame of reference).
Sample rate
The sample rate dictates the frequency at which the keys are sampled in the original raw clip. A sample rate of 30 frames per second translates in 1 second of time being divided into 30 individual frames. For a sequence with a length of 1 second, the resulting clip will have 30 frames and 31 keys.
If our game runs at a higher frame rate than our sequence sample rate (e.g. 60 FPS), we will end up interpolating between 2 keys twice as much. If in turn our games runs slower than our sample rate (e.g. 15 FPS), some keys will be skipped during playback.
Common sample rates are: 15 FPS, 20 FPS, and 30 FPS. Most games run at a frame rate of 30 FPS or 60 FPS.
Affine transform
An affine transform is a 4x4 matrix that can represent simultaneously rotation, translation, and non-uniform scaling.
Quaternion
A quaternion is a 4D complex number that can efficiently and conveniently represent a rotation in 3D space. We will not go further in depth but I will do my best to explain the relevant bits as we encounter them. Since we will mostly use them for storage, we will do very little math involving them.
The most important thing to know about them is that for a quaternion to represent a rotation, it must be normalized (unit length). And obviously, it is made up of 4 scalar float numbers.