Animation Compression: Curve Fitting
10 Dec 2016Curve fitting builds on what we last saw with linear key reduction. With it, we saw that we leveraged linear interpolation to remove keys that could easily be predicted. Curve fitting archives the same feat by using a different interpolation method: a spline function.
How It Works
The algorithm is already fairly well described by Riot Games and Bitsquid (now called Stingray) in part 1 and part 2, and as such I will not go further into details at this time.
Catmull-Rom splines are a fairly common and a solid choice to represent our curves.
In The Wild
This algorithm is again fairly popular and is used by most animation authoring software and many game engines. Sadly, I never had the chance to get my hands on a state of the art implementation of this algorithm and as such I can’t quite go as far in depth as I would otherwise like to do.
Performance
Most character animated tracks move very smoothly and approximating them with a curve is a very natural choice. In fact, clips that are authored by hand are often encoded and manipulated as a curve in Maya (or 3DS Max). If the original curves are available, we can use them as-is. This also makes the information very dense and compact. The memory footprint of curve fitting should be considerably lower than with linear key reduction but I do not have access to competitive implementations of both algorithms to make a fair comparison.
For example, take this screen capture from some animation curves in Unity:
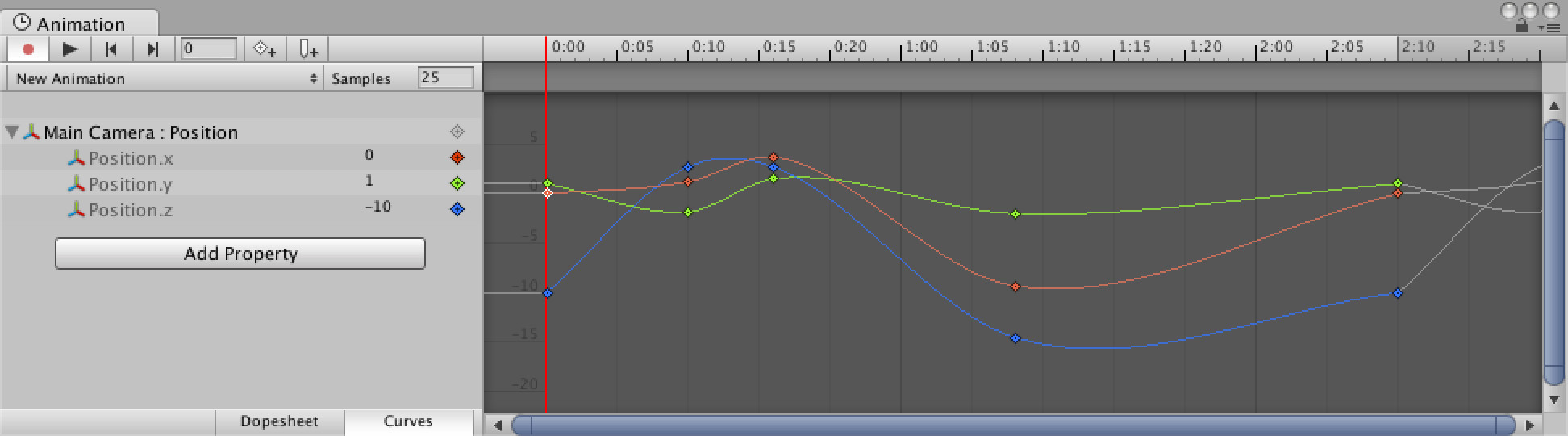
We can easily see that each track has five control points but with a total clip duration of 2.5 seconds (note that the image uses a sample rate of 25 FPS which makes the numbering a bit quirky) we would need 2.5 seconds * 30 frames/second = 75 frames to represent the same data. Even after using linear key reduction, the number of keys would remain higher than five.
As with linear key reduction, our spline control points will have time markers and most of what was mentioned previously will apply to curve fitting as well: we need to search for our neighbour control points, we need to sort our data to be cache efficient, etc.
One important distinction is that while linear key reduction only needed two keys per track to reconstruct our desired value at a particular time T, with curve fitting we might need more. For example, Catmull-Rom splines require four control points. This makes it more likely to increase the amount of cache lines we need to read when we sample our clip. For this reason, and the fact that a spline interpolation function is more expensive to execute, decompression should be slower than with linear key reduction but without access to a solid implementation, the fact that it might be slower is only an educated guess at this point.